دید کلی
بطور کلی تمام
عناصر پایدار همراه با عناصر ناپایداری که نیم عمر خیلی طویل دارند، در طبیعت یافت میشوند. لیکن از متلاشی شدن
رادیواکتیوی و تکثیر
ایزوتوپی ، تغییر فاحشی در وفور و فراوانی آنها پیدا میشود. میخواهیم بدانیم چه هستهها و عنصرهایی بیشتر در طبیعت وجود دارند.
قاعده اودو - هارکسنیس
این قاهده عنوان میدارد که عناصری با
اوزان اتمی قابل بر تقسیم بر چهار 86.5% مجموعه جرم لایه علیای
لیتوسفر را تشکیل میدهد و با توجه به ساختمان و پایداری
هسته اتمی عناصری که
عدد اتمی آنها زوج است، باید بیش از عناصری که عدد اتمی آنها فرد است وجود داشته باشند. شاهد این مدعا همانا وجود هشت عنصر
Ca , S , Mg , Si , Ni , Fe , O به میزان کلی 98.6% در
سنگهای آسمانی میباشد.
اما در همه جا بطور کلی صدق کرده که هر عنصر با عدد اتمی زوج ، فراوانتر از عناصر بلاواسطه طرفین خود که عدد اتمی آنها فرد است یافت میشود و بطور کلی مقدار آن بطور متوسط 70 برابر است و در حالات خاصی و استثنایی وفور و فراوانی هر عنصر با عدد اتمی زوج برابر معدل فراوانی دو عنصر بلاواسط آن میشود و شاهد این مدعا عناصری میباشند که از نظر
ژئوشیمی باهم بستگی دارند، یا به عبارت دیگر باهم در طبیعت یافت میشوند که مثال بارز آن ،
لانتانیدها میباشند که از لحاظ شیمیایی همگنترین گروه
جدول تناوبی و از نظر ژئوشیمی بهترین دلیل اثبات قاهده "
اودو - هارکنیس" میباشند.
منحنی تغییرات فراوانی عناصر لانتانید
وقتی منحنی تغییرات لانتانیدها را نسبت به عدد اتمی ،
Z ، برای تمام منابع ، جو خورشید ، سنگهای آسمانی و کانیها رسم میکنیم، ملاحظه میشود که تمام نقاط ماکزیمم را عناصری که عدد اتمی
Z آنها مانند
Nb , Pr , Ce و غیره زوج و نقاط مینیمم را عناصر با عدد اتمی فرد مانند
Eu , Pm , La و غیره است، اشغال کردهاند و جالبتر آنکه اغلب نقاط ماکزیمم و مینیمم بر روی یک خط قرار گرفتهاند، یعنی وفور آنها یکسان است.
استثنای قاعده اودو - هارکینس
این قاعده نیز مانند قوانین دیگر دارای استثنا میباشد و نمیتوان آن را در همه جا صادق دانست. از جمله این استثنا فراوانی بیشتر (S(Z=16 از (P(Z=15 و یا (Mg(Z=12 از Na(Z=11) و یا (Mn(Z=25 از (Cr(Z=24 است.
رابطه فراوانی عناصر با هستههای عناصر
بطور کلی فراوانی عناصر با قوانین هسته بستگی دارد و فراوانی هستههای پایدار که بحث مفصل آن به
فیزیک هسته بیشتر مربوط میشود، تابع سه عامل قرار میگیرد؛ یکی
انرژی پیوندی هسته یا انرژی غلاف بندی هسته و دیگری به عدد جرم
A یعنی مجموع
پروتونها و
نوترونهای هسته ، زیادتی و مازاد نوترونها. منظور از
انرژی پیوند هسته این است که معلوم داریم چگونه ذرات نوترون و پروتون ، اگر هسته را محض سهولت فهم متشکل از این دو ذره بدانیم، در درون هسته به هم پیوستهاند.
بر اساس تئوری نوترون و پروتون هسته اتمی ، هر هسته
دوترون ، شامل یک
نوترون و یک
پروتون است. وقتی به مقایسه جرم یک پروتون آزاد و یک نوترون آزاد با جرم یک دوترون که از اتحاد آنها بدست آمده است، میپردازیم ملاحظه میشود که مجموع جرم پروتون و نوترون برابر با 2.01712 است و حال آنکه جرم دوترون برابر با H = 2.01474 میباشد این اختلاف جرم 0.00238 بر حسب
واحد جرم اتمی amu ناشی از سنجش غیر دقیق جرم نیست، بلکه به سبب اتلاف
انرژی است که بکار رفته تا این دو ذره را به هم پیوند دهد.
محاسبه فراوانی بر حسب عدد نوترون N
اولین محاسبه ایزوتوپها در 1937 توسط "
گلدشمیت" انجام گرفت که منحنی آن قابل رسم و تفسیر است و به همان نظم و ترتیبی که در سایر منحنیها مشاهده میشود، برخورد میکنیم.
محاسبه فراوانی از روی عدد جرم
در 1937، "
گلدشیمت" به محاسبه جمع مقادیر ایزوبارها پرداخت و از روی آن توانست منحنی تغییرات
(Log S = f(A را رسم کند که
S ، مقدار وفور را نشان میدهد.
- فراوانی هستهها با عدد جرم فرد با جرم عناصر منظما تغییر میپذیرد و هستهها که در مجاورت خود ایزوبار دارند، از این قاعده مستثنا هستند. مانند Os , Te , Sn , Sr . در این حالات وقتی دو ایزوبار با یک عدد جرم A وجود دارند، جمع فراوانی ایزوبارها منظما تغییر میپذیرد.
- فراوانی هستهها با عدد جرم زوج و با اختلاف مشابه و مساوی نوترونها یعنی N - Z منظما با جرم تغییر میپذیرد. وقتی به رسم تغییرات در سه بعد (N , Z , Log S) میپردازیم، ملاحظه میشود که فراوانی تمام هستهها که عدد جرم آنها زوج است بر روی یک سطح منحنی قرار میگیرند، اما برای این قاعده هم موارد استثنایی وجود دارد.
- برای هستههای متوسط و سنگین که عدد جرم آنها فرد و یا زوج میباشد میتوان قاعده زیر را بیان داشت. برای عدد جرم ایزوباری که اختلاف نوترونی آن پایینتر است، فراوانی کمتر است. A=70 چهار مورد استثنایی 142 , 116 ,110 , 76 پیدا شده است.
نتایج بررسیها
با توجه به قواعد فراوانی مذکور در فوق که با حقایق فیزیکی هسته وفق میدهد. "
سوئس" موفق شد که به محاسبه مجدد فراوانی کهکشانی عناصر متوسط و سنگین بپردازد و مقادیری را که "
گلدشیمیت" برای لانتانیدها محاسبه کرده بود پایه و اساس قرار دهد. مقادیر حاصله کاملا با حقایقی که در مورد ساختمان ایزوتوپی عناصر کشف شده بود وفق میداد. بر حسب "
سوئس" ، مقادیر جدید فراوانی معلوم میدارد که عناصر زیر در سنگهای آسمانی نسبت به سایر منابع کهکشانی وجود ندارد و یا به مقدار خیلی ناچیز وجود دارند.
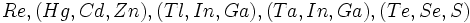
باید توجه داشت که این سه دسته عناصر از نظر شیمیایی و
آرایش الکترونی مشابه میباشند و فقدان آنها سبب واکنشهای ثانویه دیگری است. مقادیر جدید وفور که از روی منحنی نمایش آنها داده میشود، بخوبی عنوان میدارد که بعضی هستهها که عدد اتمی
Z (عدد پروتونی) و عدد نوترونی
N معین و مشخص دارند، تفوق حاصل نمودهاند. چنانچه هستههایی که
N آنها 82 , 50 , 28 , 20 و
Z آنها 82 , 74 , 50, 28 است، در
کهکشانها فراوان میباشند. به همین ترتیب هستههایی که زیادتی نوترون آنها 26 , 24 , 12 , 4 است از سایر هستهها فراوانترند
 نحوه...
نحوه...